Simulations in population genetics

PopGen summer course 2023

Authors

Martin Petr

CC BY 4.0

Published

August 2023

First things first

These slides and other resources are (and always will be) at:

github.com/bodkan/ku-popgen2023

Open this link now so you have everything at hand later.

Many problems in population genetics cannot be solved by a mathematician, no matter how gifted. [It] is already clear that computer methods are very powerful. This is good. It […] permits people with limited mathematical knowledge to work on important problems […].

James F. Crow – interview

Why use simulations?

Making sense of inferred statistics
Fitting model parameters (i.e. ABC)
Ground truth for method development

Making sense of inferred statistics

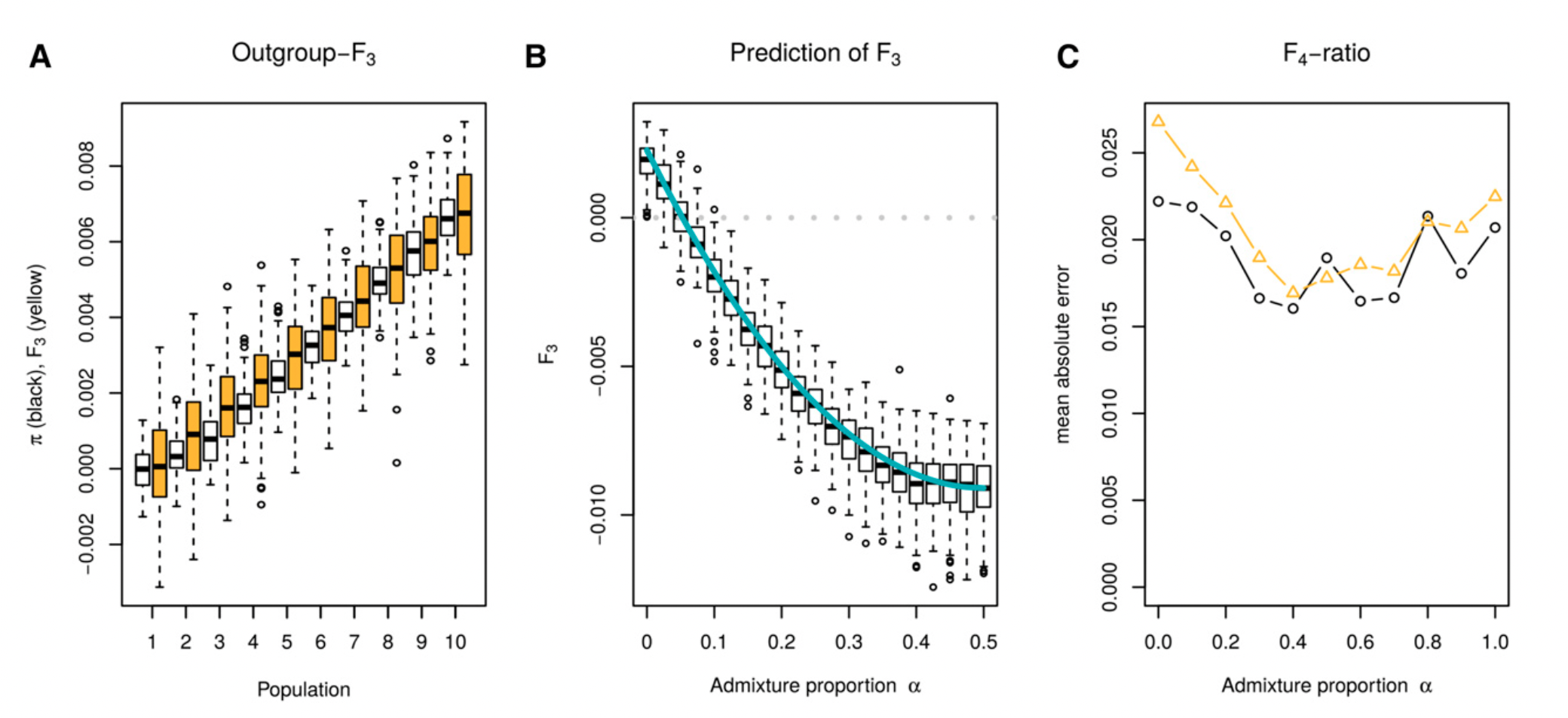
Image from Peter (2016)

Making sense of inferred statistics

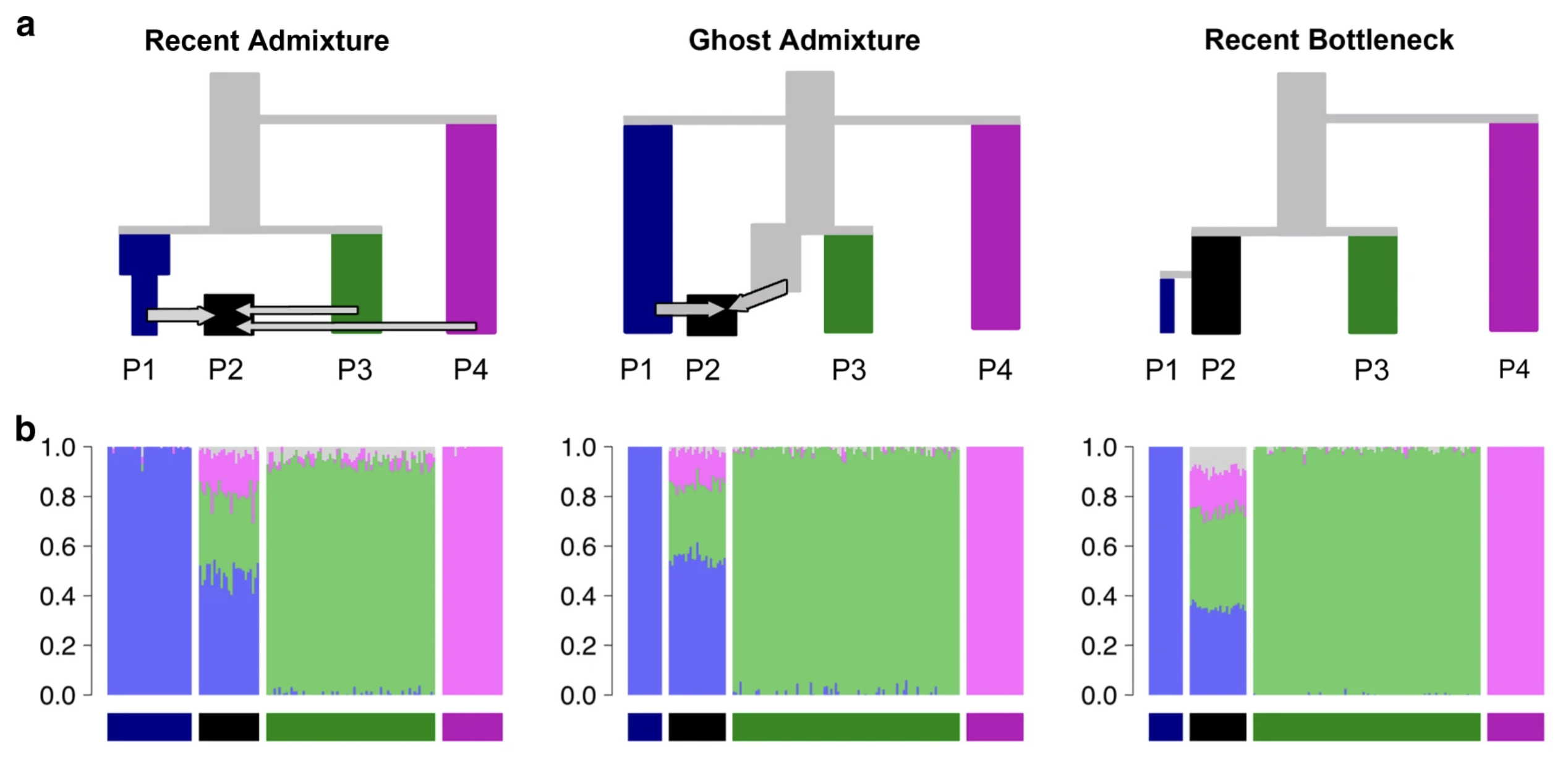
Image from Lawson et al. (2018)

Fitting model parameters (i.e. ABC)

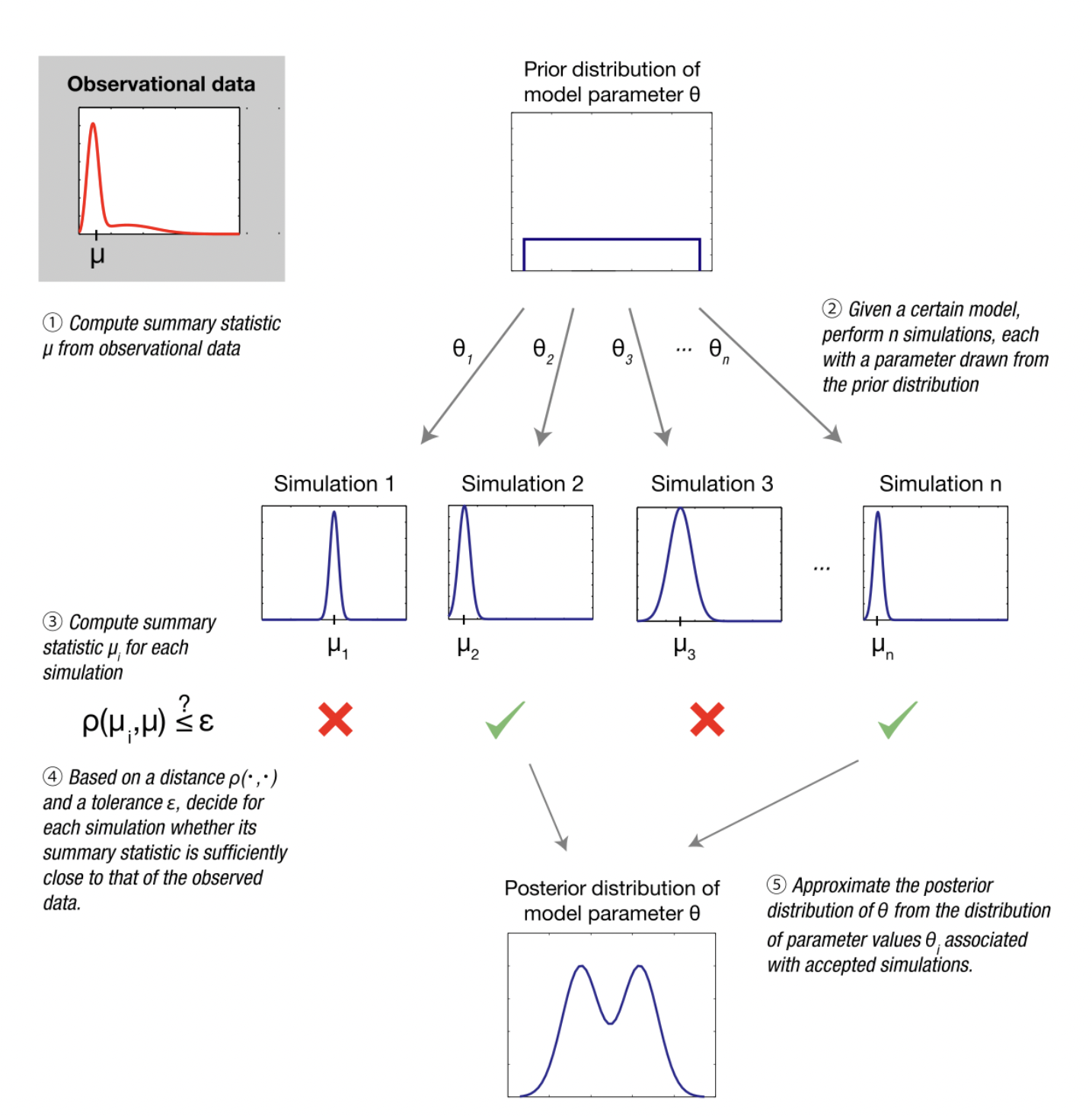
Image from Wikipedia on ABC

Ground truth for method development

Image from Schiffels and Durbin (2014)

What does it mean to simulate a genome?

How would you design an algorithm for a popgen simulation?

What minimum components are needed?

If we want to simulate population genetics

. . .

We need populations.

. . .

We need genetics.

The ‘genetics’ part…

. . .

…a linear sequence of nucleotides (a chromosome)

a list of characters (A/G/C/T nucleotides)
a list of 0 or 1 values (ancestral/derived allele),

. . .

which (maybe) mutates at a given mutation rate,

and (maybe) recombines at a certain recombination rate.

The ‘population’ part…

. . .

… a collection of individuals at a given point in time,

each carrying chromosomes inherited from its parents.

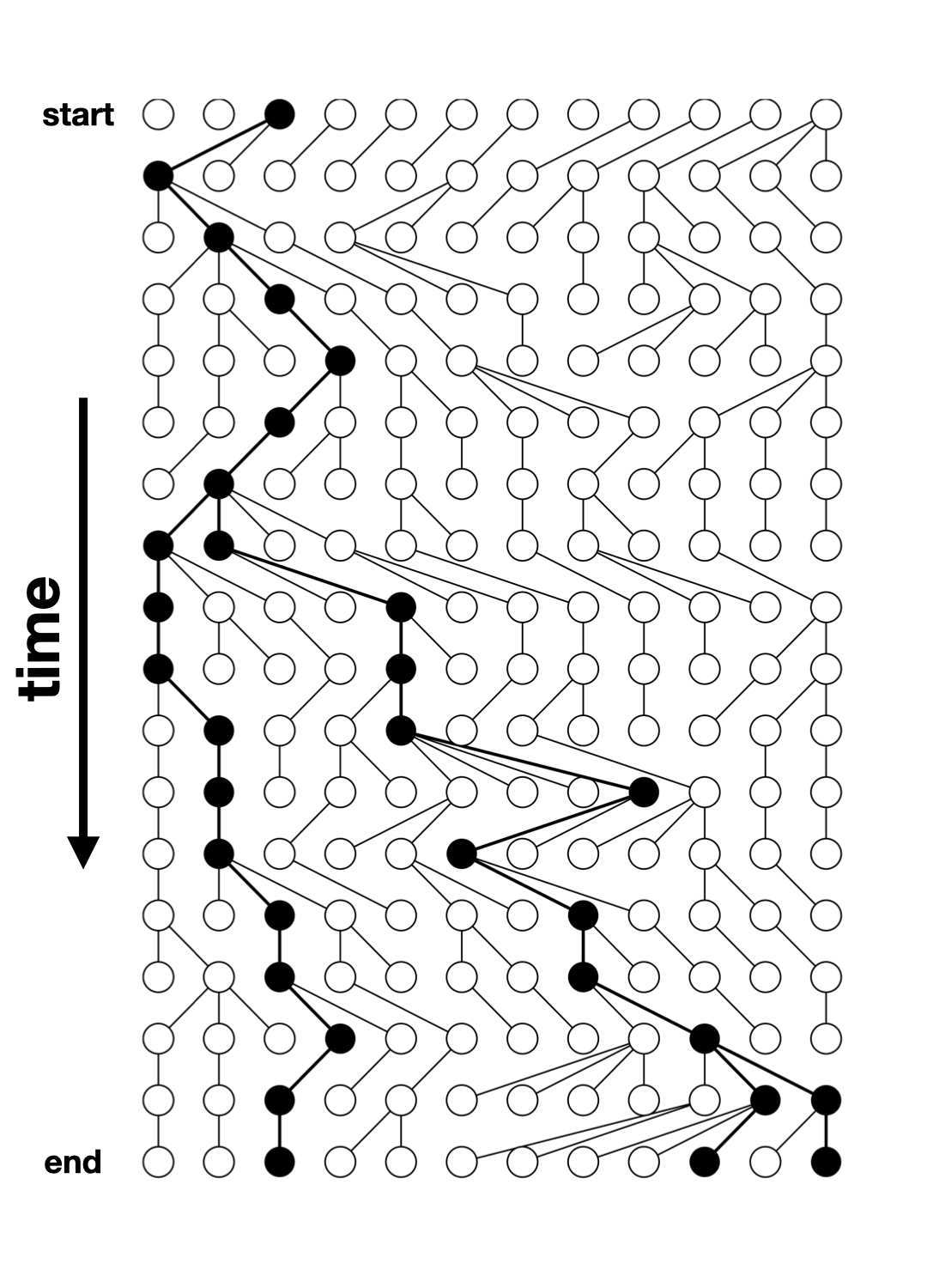
Single-locus
Wright-Fisher
simulation in R

“What is the expected trajectory of a neutral allele under the influence of genetic drift?”

From Fernando’s lecture on Monday…

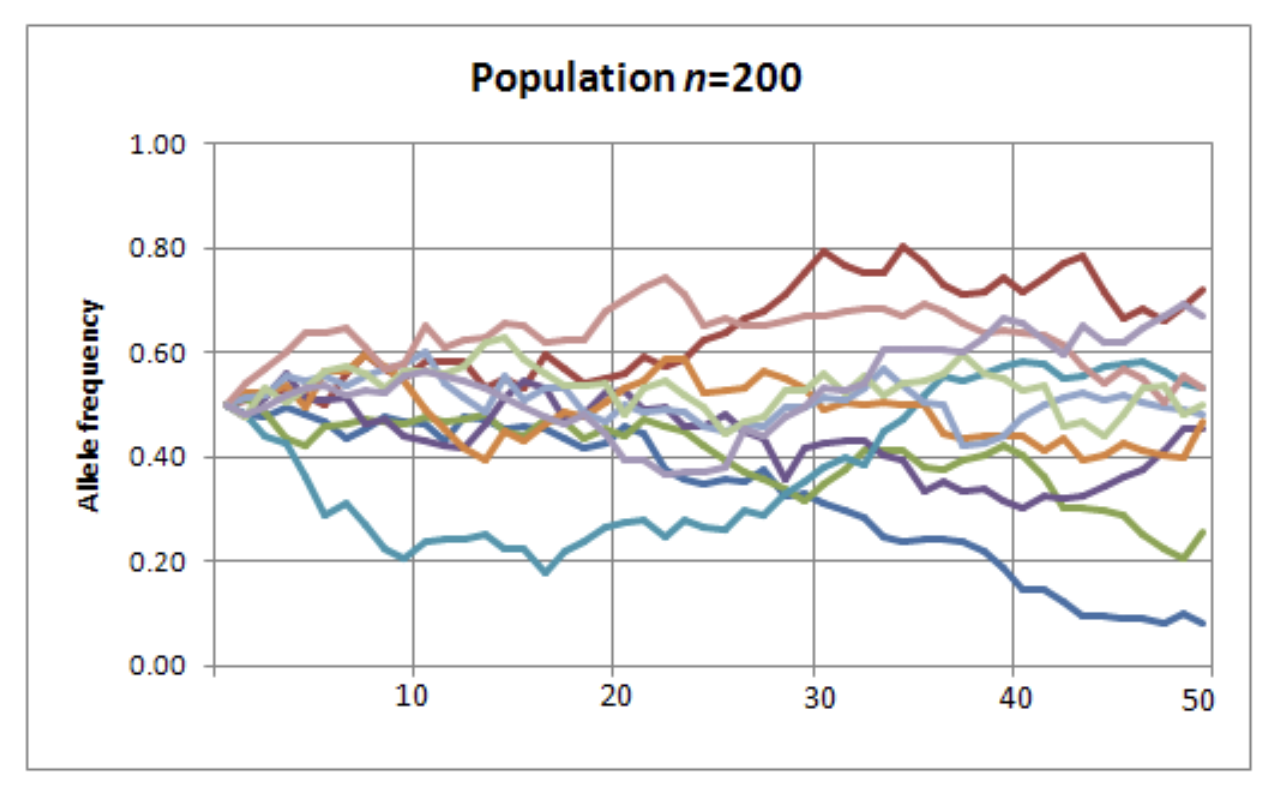
A complete Wright-Fisher simulation

p_0 <- 0.5  # initial allele frequency ("50% marbles" from lecture #1)
N   <- 500  # number of chromosomes in a population
T   <- 2000 # number of generations to simulate

# a vector for storing frequencies over time
p_trajectory <- p_0 

# in each generation:
for (gen_i in 2:T) {
  # get frequency in the previous generation
  p_prev <- p_trajectory[gen_i - 1] 

  # calculate new frequency ("sampling marbles from a jar")
  p_trajectory[gen_i] <- rbinom(1, N, p_prev) / N 
}

plot(p_trajectory)

\(N\) = 500, \(p_0 = 0.5\)

Code

plot(p_trajectory, type = "l", ylim = c(0, 1),
     xlab = "generations", ylab = "allele frequency")
abline(h = p_0, lty = 2, col = "red")

Let’s make it a function

Input: \(p_0\), \(N\), and the number of generations

Output: allele frequency trajectory vector

simulate <- function(p_0, N, T) {
  p_trajectory <- p_0

  for (gen_i in 2:T) {
    p_prev <- p_trajectory[gen_i - 1]
    p <- rbinom(1, N, p_prev) / N
    p_trajectory[gen_i] <- p
  }

  return(p_trajectory)
}

. . .

And then:

simulate(p_0 = 0.5, N = 1000, T = 10)

 [1] 0.500 0.471 0.499 0.517 0.529 0.519 0.518 0.525 0.520 0.516

\(N\) = 500, \(p_0 = 0.5\) (20 replicates)

Code

reps <- replicate(20, simulate(N = 500, p_0 = 0.5, T = 2000))

matplot(reps, ylim = c(0, 1), xlab = "generations", ylab = "allele frequency", type = "l", lty = 1)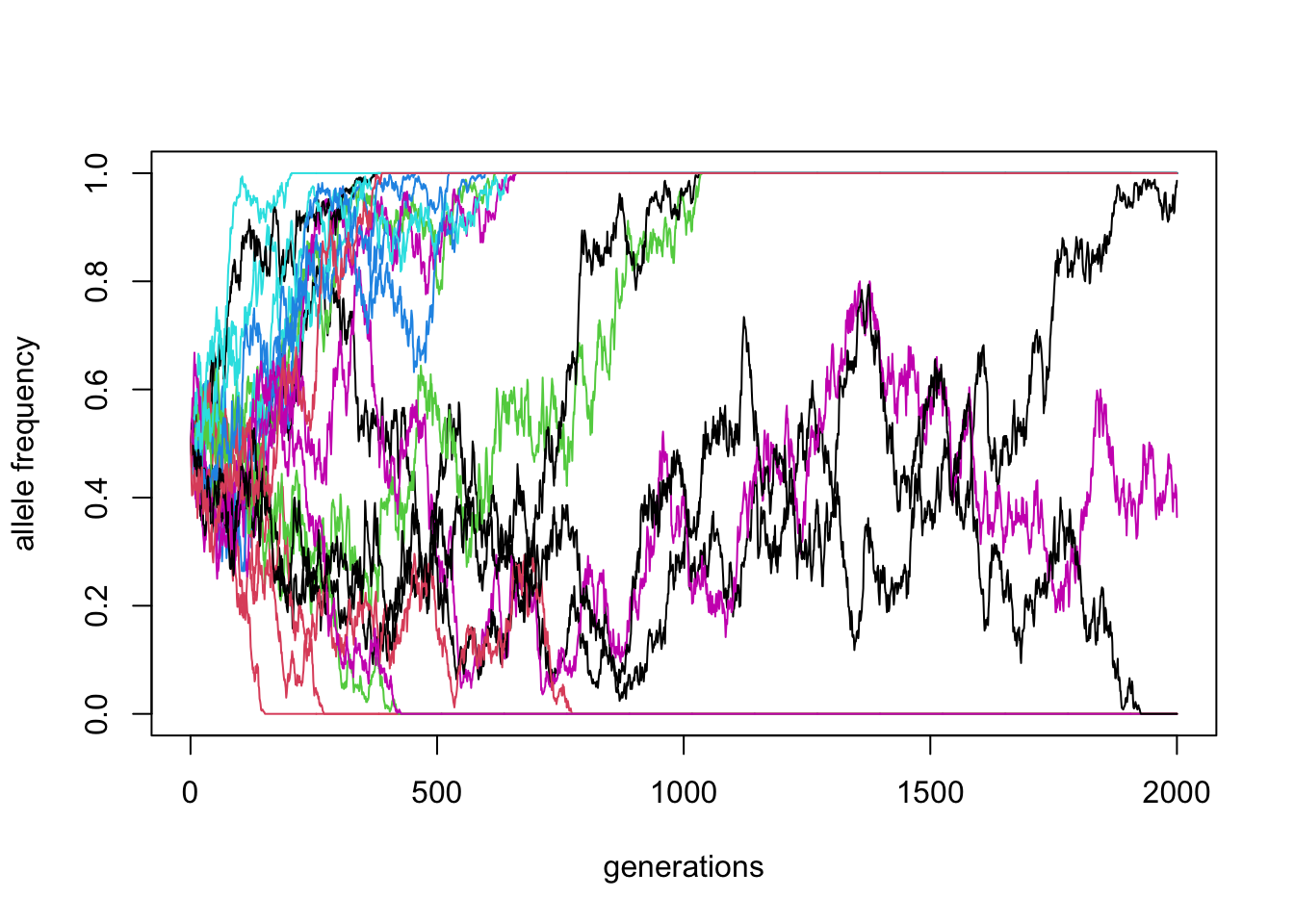

\(N\) = 1000, \(p_0 = 0.5\) (20 replicates)

Code

reps <- replicate(20, simulate(N = 1000, p_0 = 0.5, T = 2000))

matplot(reps, ylim = c(0, 1), xlab = "generations", ylab = "allele frequency", type = "l", lty = 1)

\(N\) = 5000, \(p_0 = 0.5\) (20 replicates)

Code

reps <- replicate(20, simulate(N = 5000, p_0 = 0.5, T = 2000))

matplot(reps, ylim = c(0, 1), xlab = "generations", ylab = "allele frequency", type = "l", lty = 1)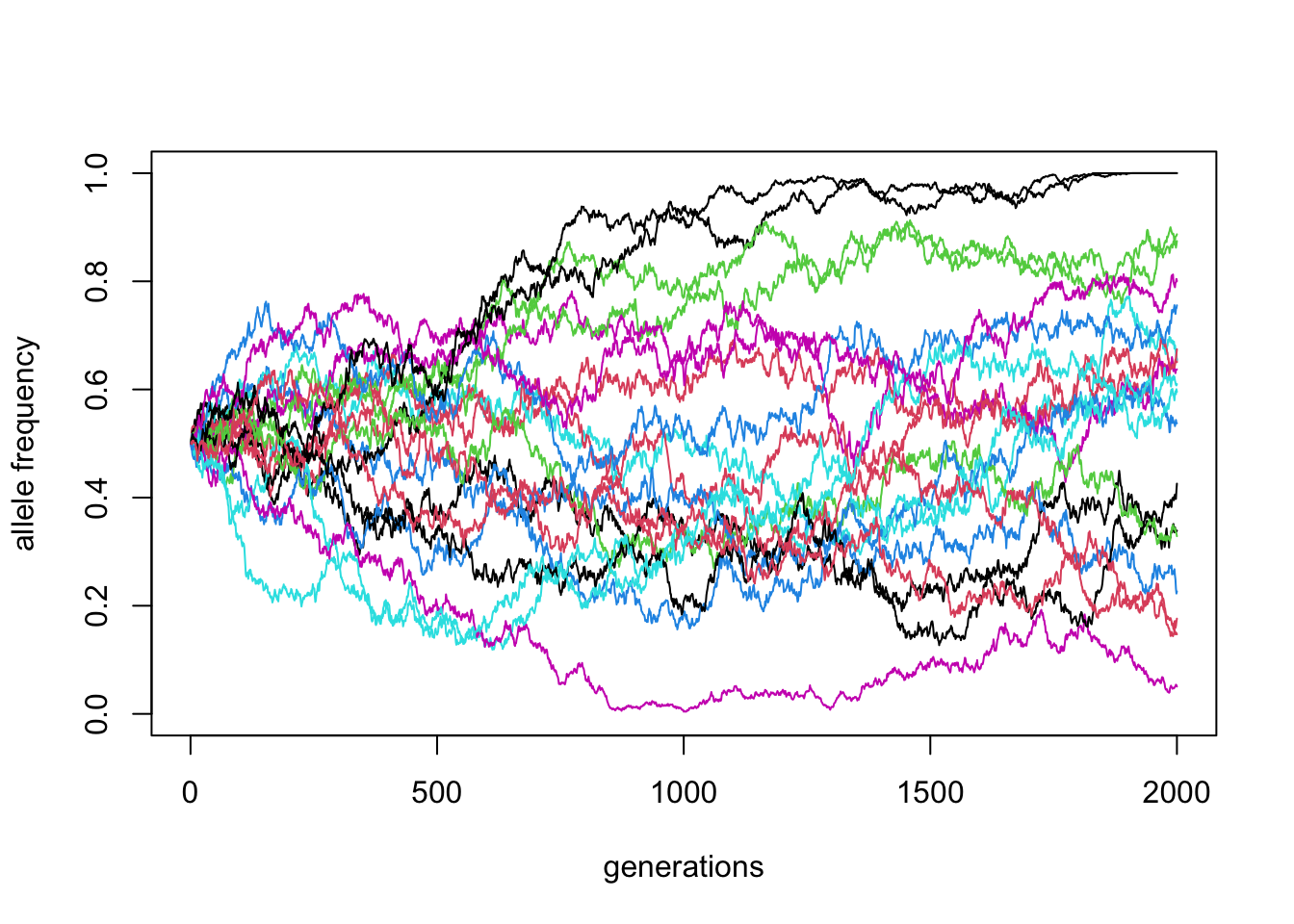

\(N\) = 10000, \(p_0 = 0.5\) (20 replicates)

Code

reps <- replicate(20, simulate(N = 10000, p_0 = 0.5, T = 2000))

matplot(reps, ylim = c(0, 1), xlab = "generations", ylab = "allele frequency", type = "l", lty = 1)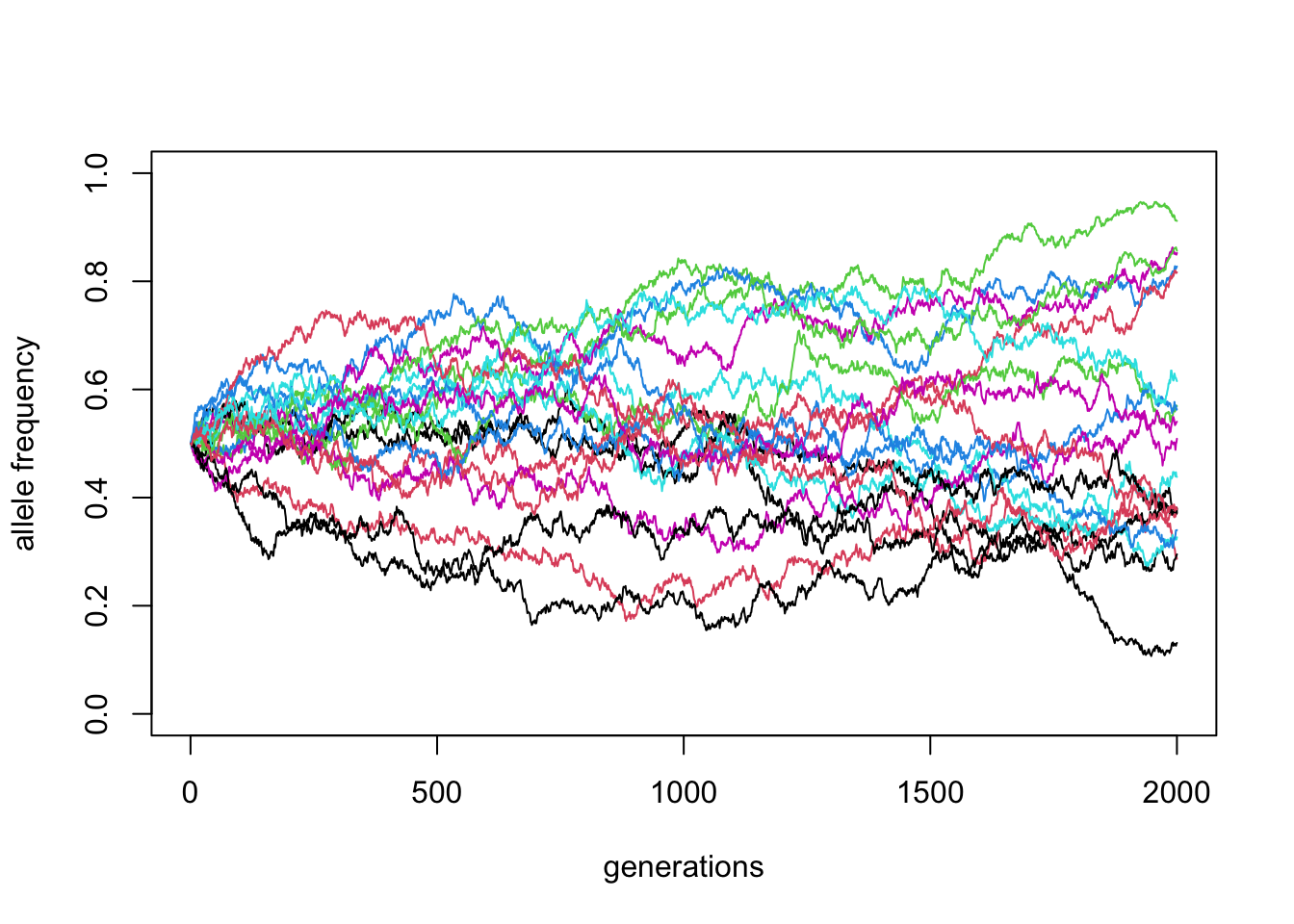

\(N\) = 10000, \(p_0 = 0.5\) (100 replicates)

Code

reps <- replicate(100, simulate(N = 10000, p_0 = 0.5, T = 30000))

matplot(reps, ylim = c(0, 1), xlab = "generations", ylab = "allele frequency", type = "l", lty = 1)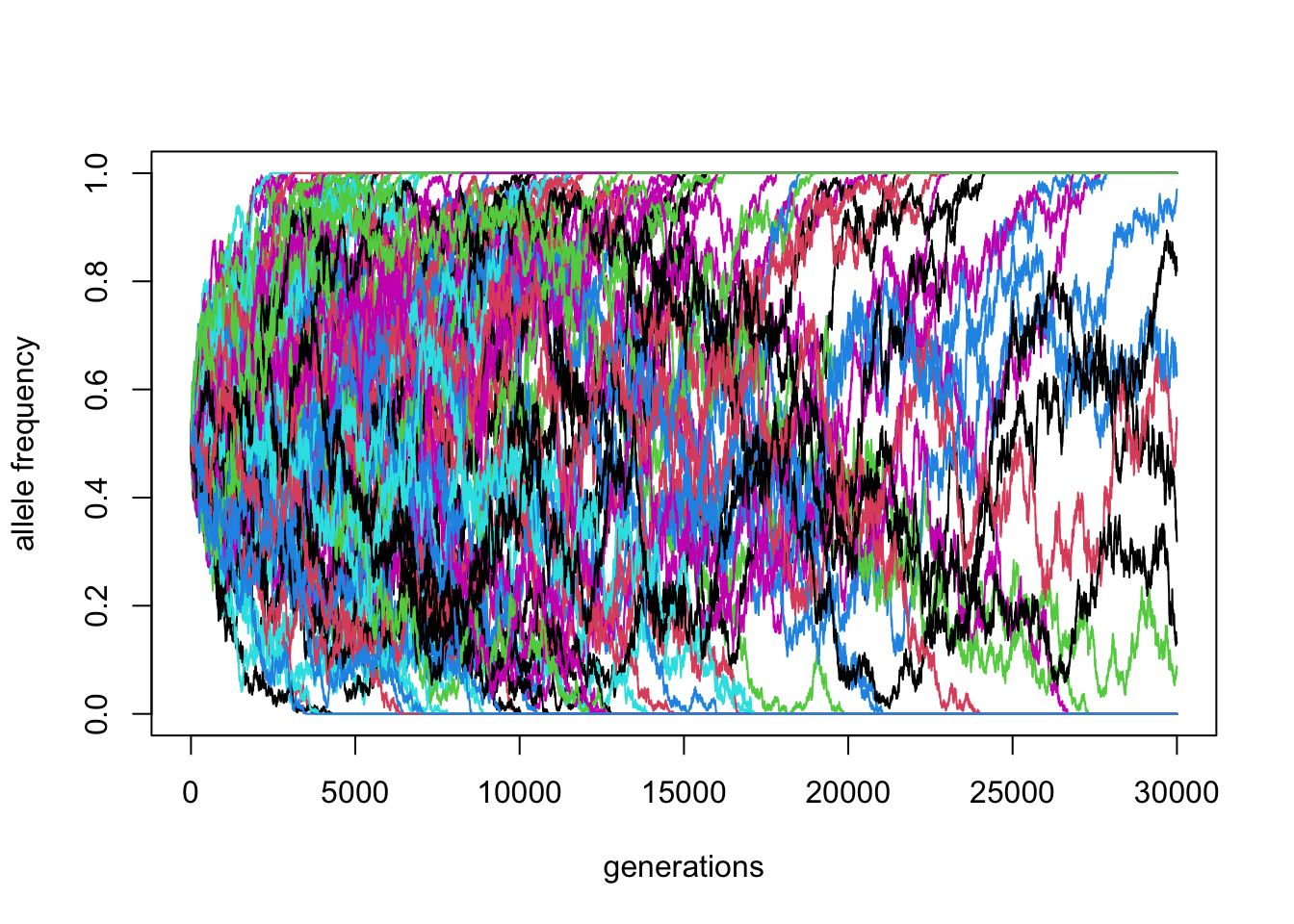

\(N\) = 10000, \(p_0 = 0.5\) (100 replicates)

Code

factors <- MASS::fractions(c(3, 2, 1, 1/2, 1/5, 1/10))
matplot(reps, ylim = c(0, 1), xlab = "generations", ylab = "allele frequency", type = "l", lty = 1)
abline(v = 10000 * factors, lwd = 5)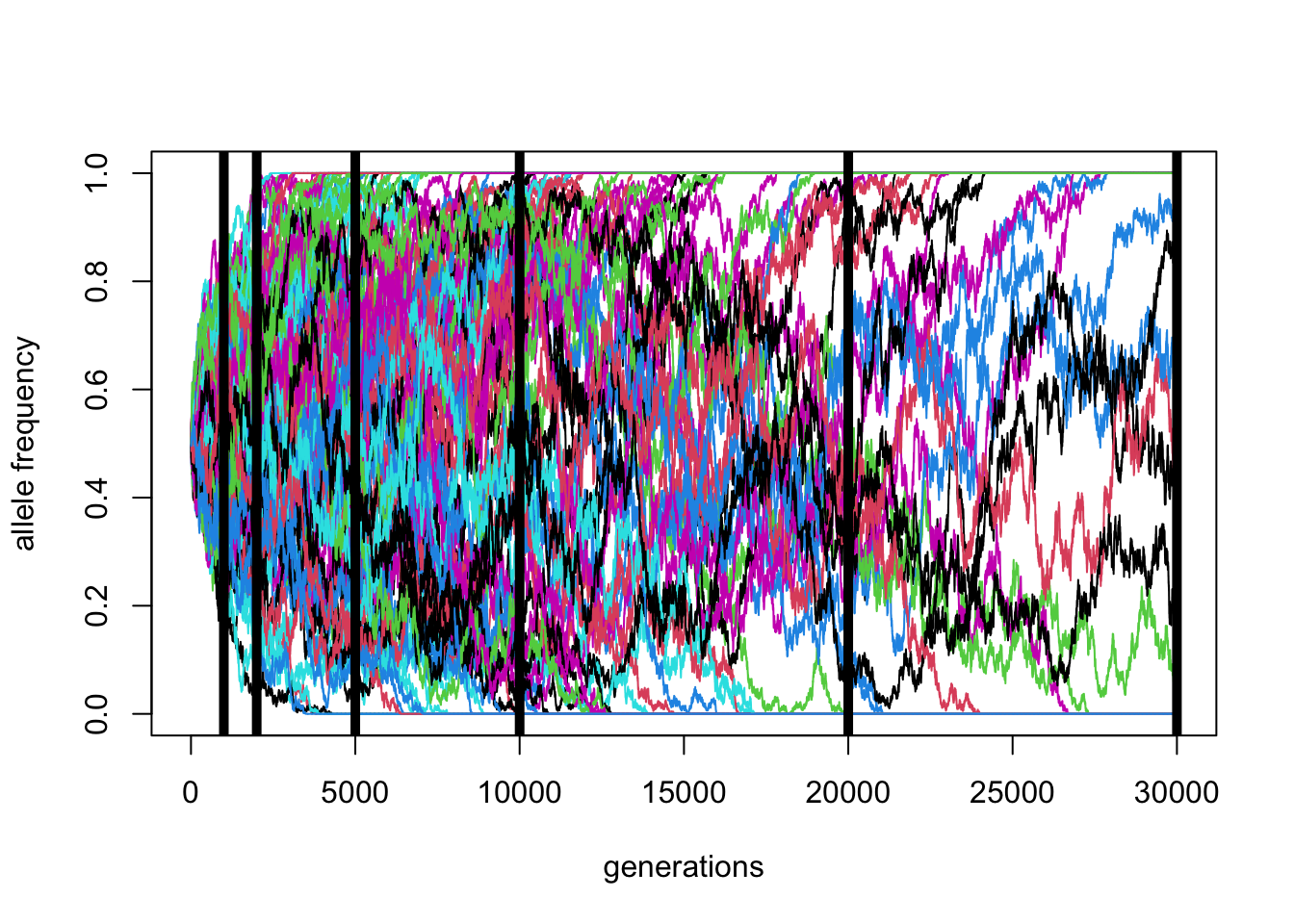

Expected allele frequency distribution

Code

library(ggplot2)
library(dplyr)


Attaching package: 'dplyr'

The following objects are masked from 'package:stats':

    filter, lag

The following objects are masked from 'package:base':

    intersect, setdiff, setequal, union

Code

library(parallel)

if (!file.exists("diffusion.rds")) {
p_0 <- 0.5
N <- 10000
factors <- MASS::fractions(c(3, 2, 1, 1/2, 1/5, 1/10))

final_frequencies <- parallel::mclapply(
  seq_along(factors), function(i) {
    f <- factors[i]
    t <- as.integer(N * f)
    # get complete trajectories as a matrix (each column a single trajectory)
    reps <- replicate(10000, simulate(N = N, p_0 = p_0, T = t))
    # only keep the last slice of the matrix with the final frequencies
    data.frame(
      t = sprintf("t = %s * N", f),
      freq = reps[t, ]
    )
  },
  mc.cores = parallel::detectCores()
) %>% do.call(rbind, .)
final_frequencies$t <- forcats::fct_rev(forcats::fct_relevel(final_frequencies$t, sprintf("t = %s * N", factors)))
saveRDS(final_frequencies, "diffusion.rds")
} else {
  final_frequencies <- readRDS("diffusion.rds")
}

final_frequencies %>% .[.$freq > 0 & .$freq < 1, ] %>%
ggplot() +
  geom_histogram(aes(freq, y = after_stat(density), fill = t), position = "identity", bins = 100, alpha = 0.75) +
  labs(x = "allele frequency") +
  coord_cartesian(ylim = c(0, 3)) +
  facet_grid(t ~ .) +
  guides(fill = guide_legend(sprintf("time since\nthe start\n[assuming\nN = %s]", N))) +
  theme_minimal() +
  theme(strip.text.y = element_blank(),
        axis.title.x = element_text(size = 15),
        axis.title.y = element_text(size = 15),
        axis.text.x = element_text(size = 15),
        axis.text.y = element_text(size = 15),
        legend.title = element_text(size = 15),
        legend.text = element_text(size = 15))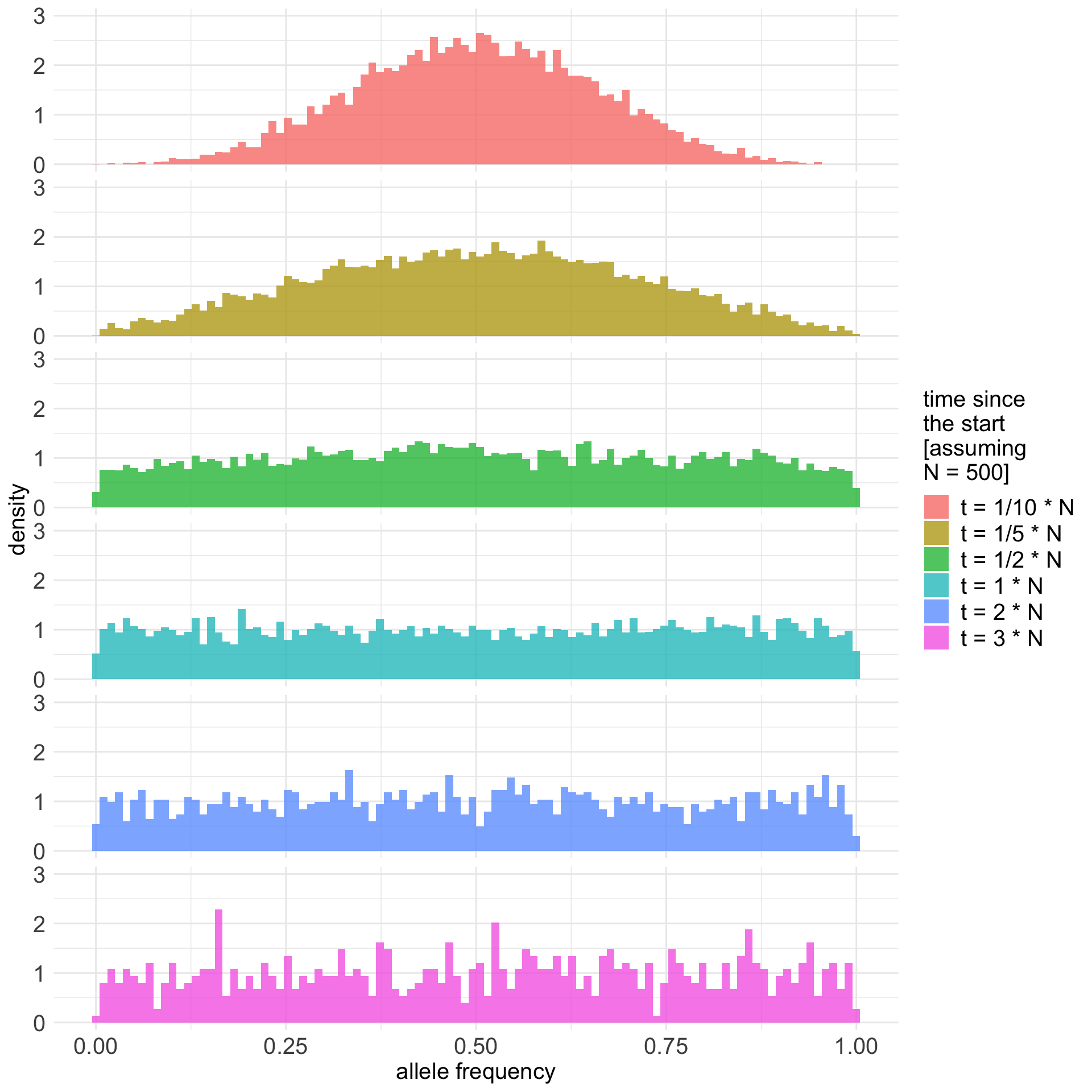

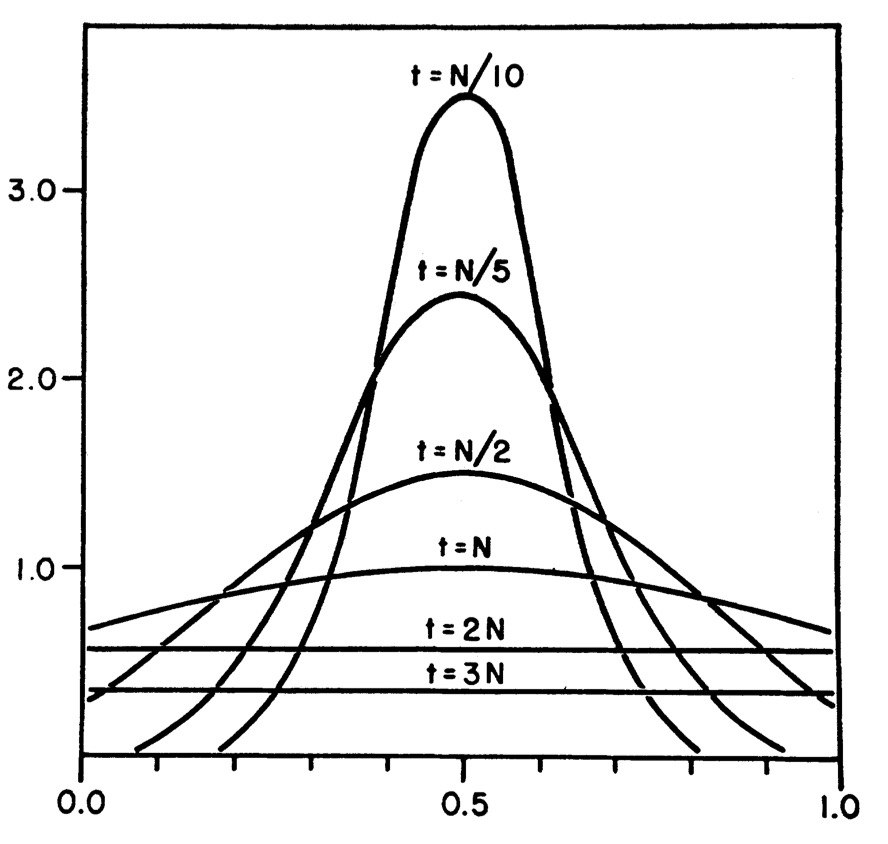
*“Diffusion Models in Population Genetics”*, Kimura (1964)

But now for something
completely different.

Let’s talk about
real simulations.

There are many simulation tools

The most famous and widely used are SLiM and msprime.

They are very powerful but both require:

quite a bit of programming knowledge,
a lot of code for non-trivial simulations (🐛🪲🐜).

The exercises will focus on the slendr
popgen simulation toolkit for R.

But let’s look at SLiM and msprime at least a little bit.

What is SLiM?

A forward-time simulator

It’s fully programmable!

Massive library of functions for:
- demographic events
- various mating systems
- selection, quantitative traits, …

> 700 pages long manual!

Simple neutral simulation in SLiM

initialize() {
    // create a neutral mutation type
    initializeMutationType("m1", 0.5, "f", 0.0);
    // initialize 1Mb segment
    initializeGenomicElementType("g1", m1, 1.0);
    initializeGenomicElement(g1, 0, 999999);
    // set mutation rate and recombination rate of the segment
    initializeMutationRate(1e-8);
    initializeRecombinationRate(1e-8);
}

// create an ancestral population p1 of 10000 diploid individuals
1 early() { sim.addSubpop("p1", 10000); }

// in generation 1000, create two daughter populations p2 and p3
1000 early() {
    sim.addSubpopSplit("p2", 5000, p1);
    sim.addSubpopSplit("p3", 1000, p1);
}

// in generation 10000, stop the simulation and save 100 individuals
// from p2 and p3 to a VCF file
10000 late() {
    p2_subset = sample(p2.individuals, 100);
    p3_subset = sample(p3.individuals, 100);
    c(p2_subset, p3_subset).genomes.outputVCF("/tmp/slim_output.vcf.gz");
    sim.simulationFinished();
    catn("DONE!");
}

What is msprime?

A Python module for writing coalescent simulations

Extremely fast (genome-scale, population-scale data)

You must know Python fairly well to build complex models

Simple simulation using msprime

import msprime

demography = msprime.Demography()
demography.add_population(name="A", initial_size=10_000)
demography.add_population(name="B", initial_size=5_000)
demography.add_population(name="C", initial_size=1_000)
demography.add_population_split(time=1000, derived=["A", "B"], ancestral="C")

ts = msprime.sim_ancestry(
  sequence_length=10e6,
  recombination_rate=1e-8,
  samples={"A": 100, "B": 100},
  demography=demography
)

www.slendr.net

Why a new package?

Spatial simulations!

Why a new package?

Most researchers are not expert programmers
All but the most trivial simulations require lots of code

90% ^{[citation needed]} of simulations are basically the same!
- create populations (splits and \(N_e\) changes)
- specify if/how they should mix (rates and times)

Lot of code duplication across projects

slendr makes “standard” demographic simulations trivial
and unlocks new kinds of spatial simulations

Let’s get started

Everything we do will be in R

Always start your R scripts with this (*):

library(slendr)

The legacy packages maptools, rgdal, and rgeos, underpinning the sp package,
which was just loaded, will retire in October 2023.
Please refer to R-spatial evolution reports for details, especially
https://r-spatial.org/r/2023/05/15/evolution4.html.
It may be desirable to make the sf package available;
package maintainers should consider adding sf to Suggests:.
The sp package is now running under evolution status 2
     (status 2 uses the sf package in place of rgdal)

init_env()

The interface to all required Python modules has been activated.

My solutions will also use these two packages:

library(ggplot2)
library(dplyr)

(*) You can safely ignore the message about missing SLiM.

Typical steps of a slendr R workflow

creating populations
scheduling population splits
programming \(N_e\) size changes
encoding gene-flow events
simulation sequence of a given size
computing statistics from simulated outputs

Creating a `population()`

Each needs a name, size and time of appearance:

pop1 <- population("pop1", N = 1000, time = 1)

. . .

This creates a normal R object. Typing it out gives a summary:

pop1

slendr 'population' object 
-------------------------- 
name: pop1 
non-spatial population
stays until the end of the simulation

population history overview:
  - time 1: created as an ancestral population (N = 1000)

Programming population splits

Splits are indicated by the parent = <pop> argument:

pop2 <- population("pop2", N = 100, time = 50, parent = pop1)

. . .

The split is reported in the “historical summary”:

pop2

slendr 'population' object 
-------------------------- 
name: pop2 
non-spatial population
stays until the end of the simulation

population history overview:
  - time 50: split from pop1 (N = 100)

Scheduling resize events – `resize()`

Step size decrease:

pop1 <- population("pop1", N = 1000, time = 1)
pop1_step <- resize(pop1, N = 100, time = 500, how = "step")

Exponential increase:

pop2 <- population("pop2", N = 100, time = 50, parent = pop1)
pop2_exp <- resize(pop2, N = 10000, time = 500, end = 2000, how = "exponential")

Tidyverse-style pipe `%>%` interface

A more concise way to express the same thing as before.

Step size decrease:

pop1 <-
  population("pop1", N = 1000, time = 1) %>%
  resize(N = 100, time = 500, how = "step")

Exponential increase:

pop2 <-
  population("pop2", N = 1000, time = 1) %>%
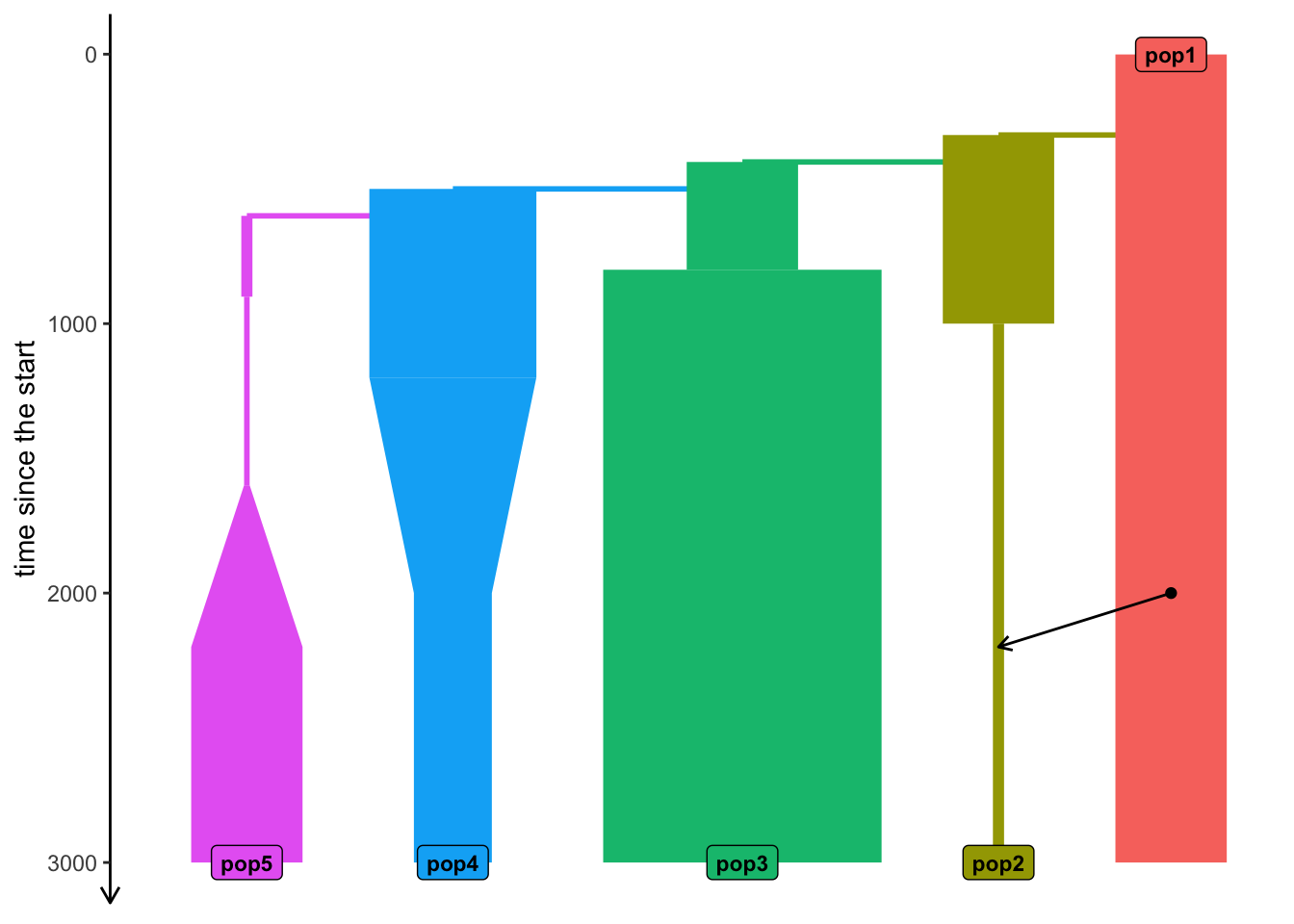
  resize(N = 10000, time = 500, end = 2000, how = "exponential")

A more complex model

pop1 <- population("pop1", N = 1000, time = 1)

pop2 <-
  population("pop2", N = 1000, time = 300, parent = pop1) %>%
  resize(N = 100, how = "step", time = 1000)

pop3 <-
  population("pop3", N = 1000, time = 400, parent = pop2) %>%
  resize(N = 2500, how = "step", time = 800)

pop4 <-
  population("pop4", N = 1500, time = 500, parent = pop3) %>%
  resize(N = 700, how = "exponential", time = 1200, end = 2000)

pop5 <-
  population("pop5", N = 100, time = 600, parent = pop4) %>%
  resize(N = 50, how = "step", time = 900) %>%
  resize(N = 1000, how = "exponential", time = 1600, end = 2200)

Each object carries its history!

pop5

slendr 'population' object 
-------------------------- 
name: pop5 
non-spatial population
stays until the end of the simulation

population history overview:
  - time 600: split from pop4 (N = 100)
  - time 900: resize from 100 to 50 individuals
  - time 1600-2200: exponential resize from 50 to 1000 individuals

Gene flow / admixture

We can schedule gene_flow() from pop1 into pop2 with:

gf <- gene_flow(from = pop1, to = pop2, start = 2000, end = 2200, rate = 0.13)

. . .

Here rate = 0.13 means 13% migrants over the given time window will come from “pop1” into “pop2”.

. . .

Multiple gene-flow events can be gathered in a list:

gf <- list(
  gene_flow(from = pop1, to = pop2, start = 500, end = 600, rate = 0.13),
  gene_flow(from = ..., to = ..., start = ..., end = ..., rate = ...),
  ...
)

Last step before simulation: `compile_model()`

model <- compile_model(
  list(pop1, pop2, pop3, pop4, pop5),
  generation_time = 1,
  simulation_length = 3000,
  direction = "forward"
)

Compilation takes a list of model components, performs internal consistency checks, returns a single model object.

Last step before simulation: `compile_model()`

model <- compile_model(
  list(pop1, pop2, pop3, pop4, pop5),
  gene_flow = gf,      # <----- in case our model includes gene flow
  generation_time = 1,
  simulation_length = 3000,
  direction = "forward"
)

Gene flow(s) that we programmed are included
via the gene_flow argument.

Model summary

Typing the compiled model into R prints a brief summary:

model

slendr 'model' object 
--------------------- 
populations: pop1, pop2, pop3, pop4, pop5 
geneflow events: 1 
generation time: 1 
time direction: forward 
total running length: 3000 model time units
model type: non-spatial

configuration files in: /private/var/folders/d_/hblb15pd3b94rg0v35920wd80000gn/T/RtmpqrQYCe/fileadfc7176d62f

Model visualization

plot_model(model, proportions = TRUE)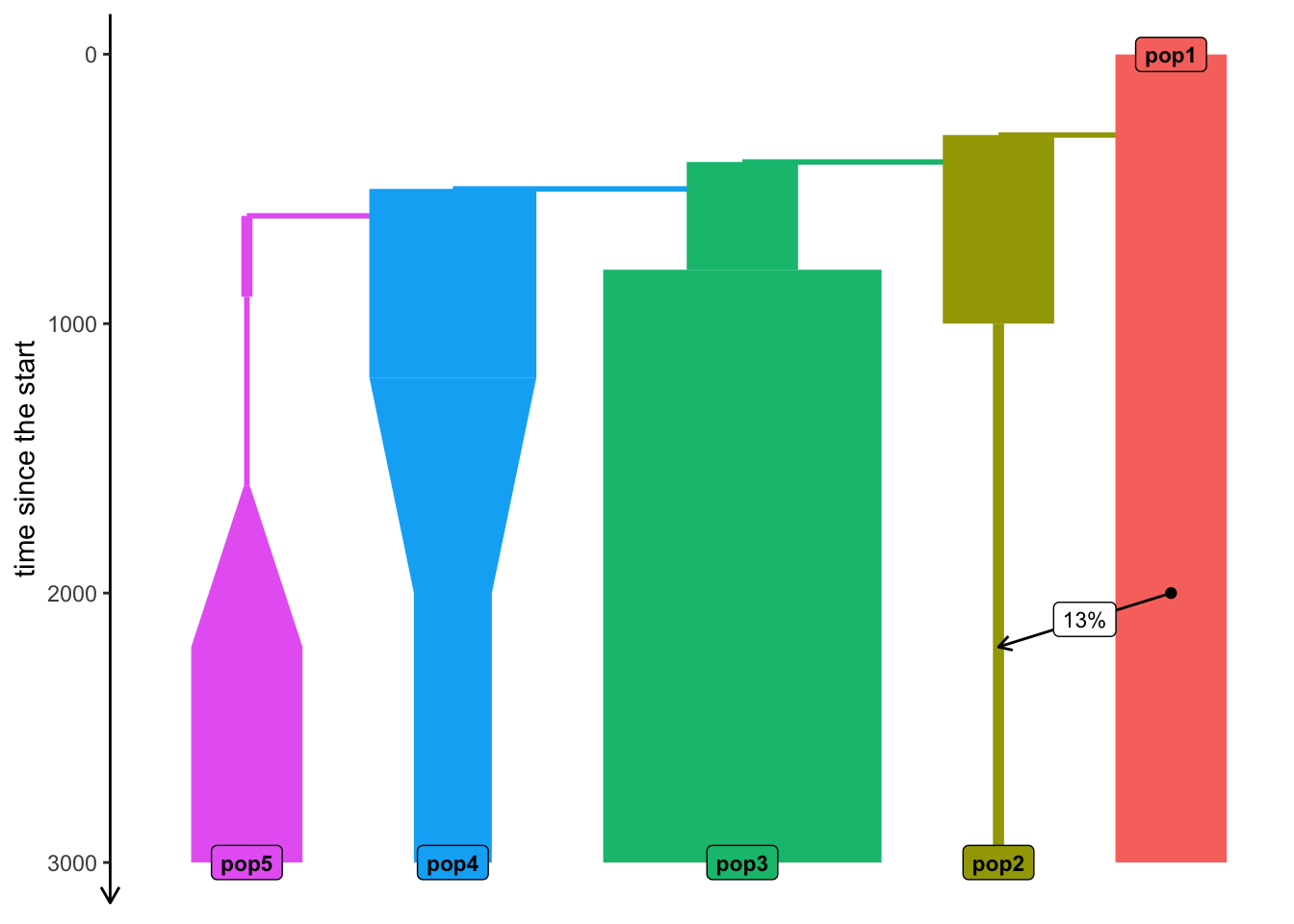

Exercise #1

Go to the lecure & exercises page

Link: github.com/bodkan/ku-popgen2023

Open the relevant red-highlighted links:

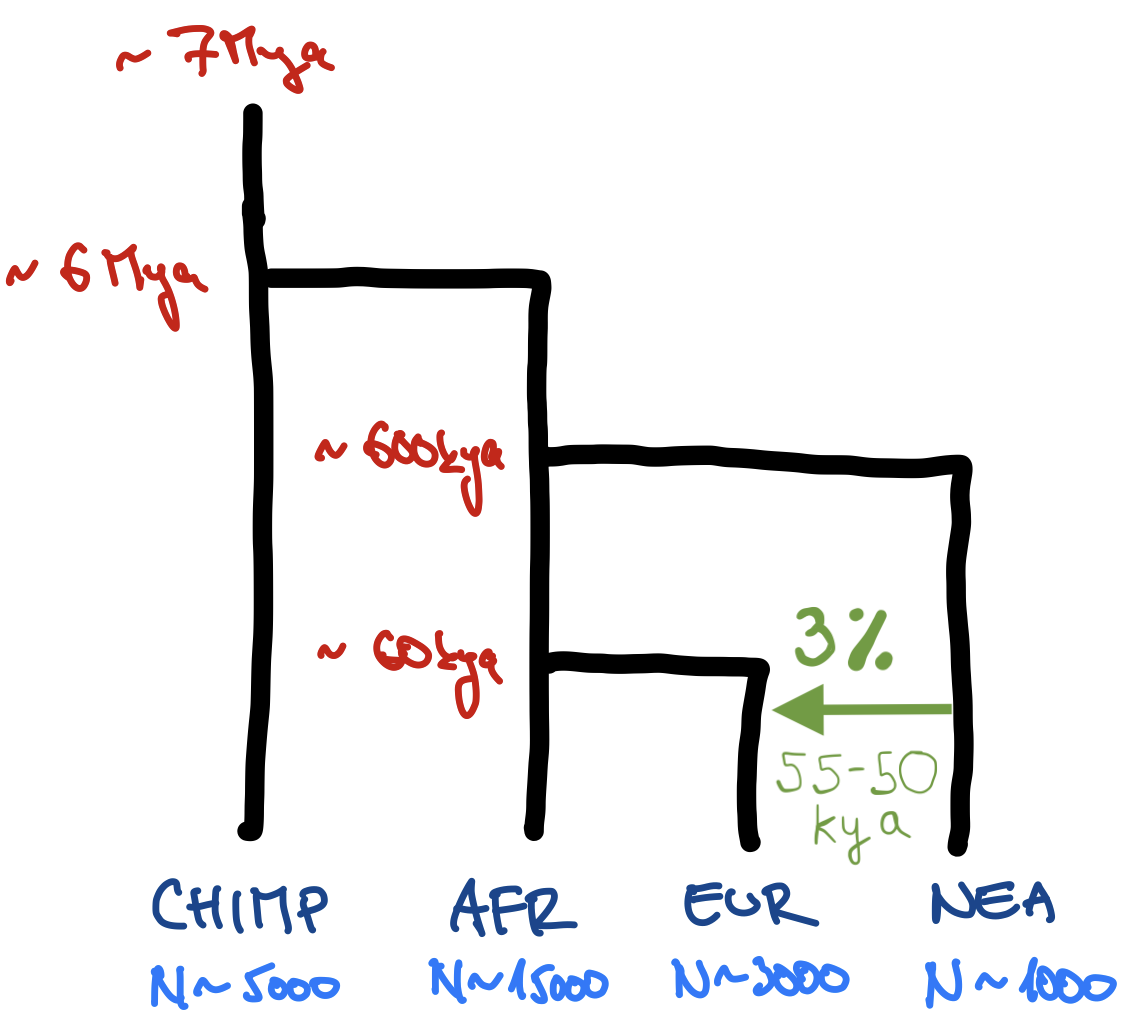
Exercise #1: write this model in slendr

Start a model1.R script in RStudio with this “template”:

library(slendr); init_env()

<... population definitions ...>
<... gene flow definition ...>

model <- compile_model(
  populations = list(...),
  gene_flow = <...>,
  generation_time = 30
)

plot_model(model) # verify visually

Note: You can also give time in units of “years ago”, just write them in a decreasing order (7Mya → 6Mya → …, as shown above). In that case, don’t set simulation_length.

Exercise #1 (bonus): your own model

Program a model for an organism that you study.

If applicable, include bottlenecks, expansions, etc. Don’t hesitate to make it as complex as you want.

Use plot_model() to check your model visually.

Save it in a different R script—you will use it in a later exercise.

Exercise #1: solution

See ex1.R on GitHub for a solution.

So, now we can
write a `model`

How do we simulate from it?

slendr has two built-in simulation “engine scripts”:

SLiM engine (source)
msprime engine (source)

They are designed to understand slendr models.

. . .

All you need to simulate data is this one line of code:

ts <- msprime(model, sequence_length = 100e6, recombination_rate = 1e-8)

**You don’t have to write msprime or SLiM code!**

The output of a slendr simulation is a tree sequence (`ts`)

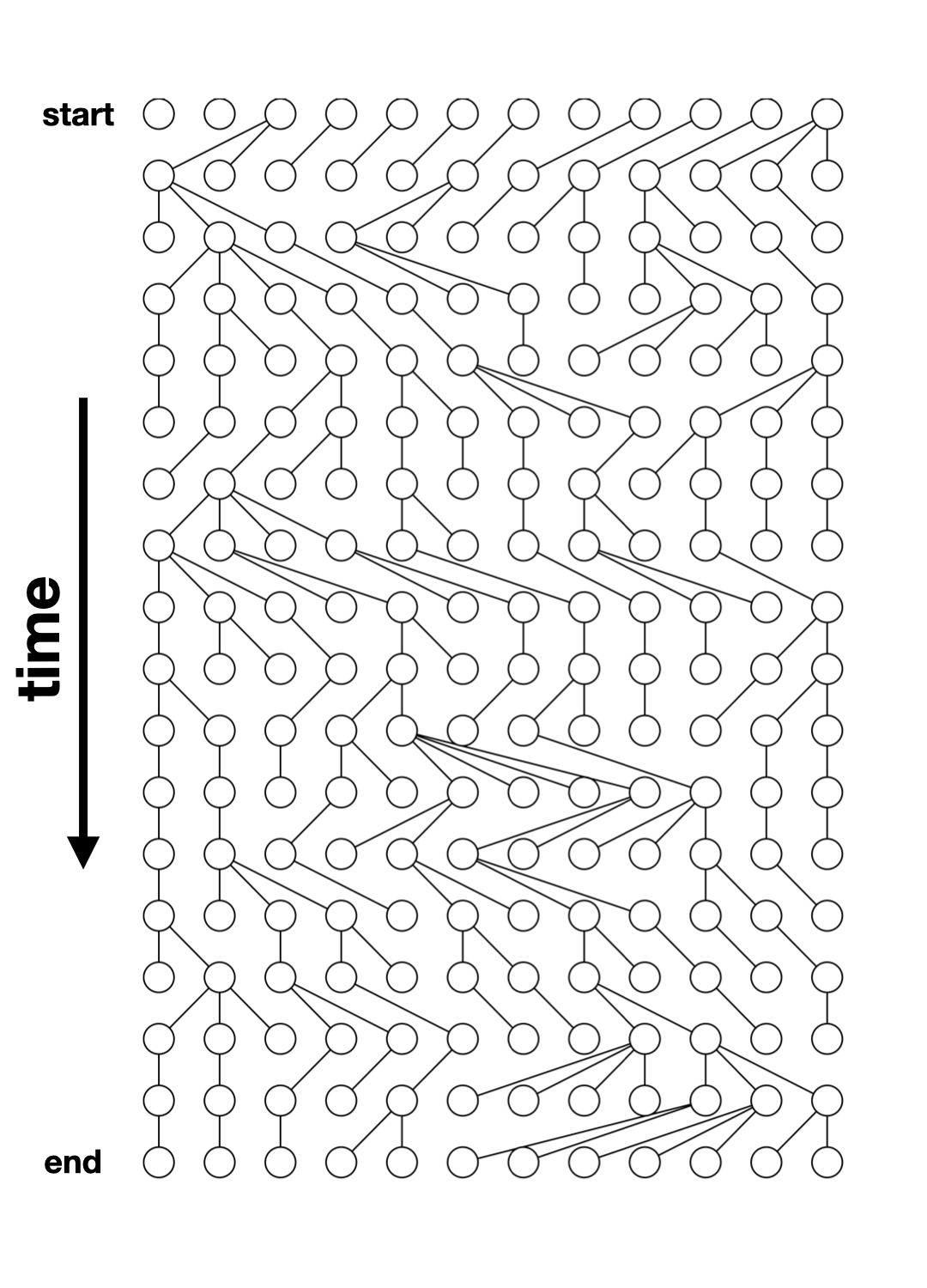
What is tree sequence?

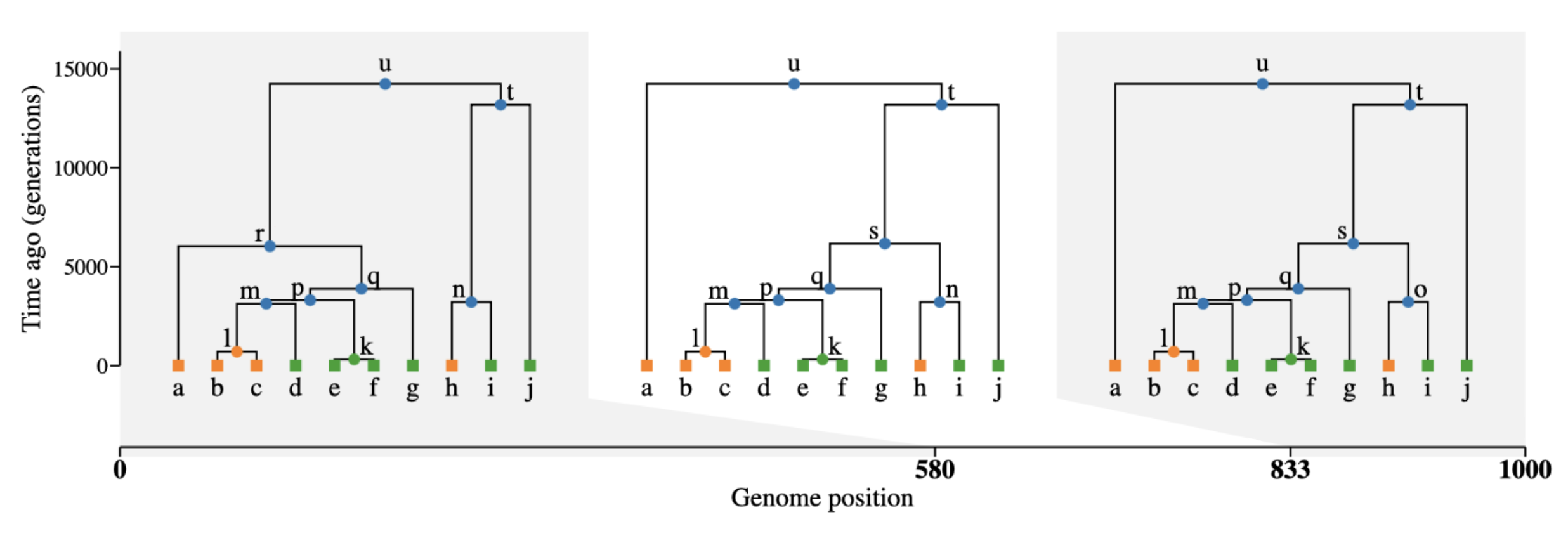
a record of full genetic ancestry of a set of samples
an encoding of DNA sequence carried by those samples
an efficient analysis framework

Why tree sequence?

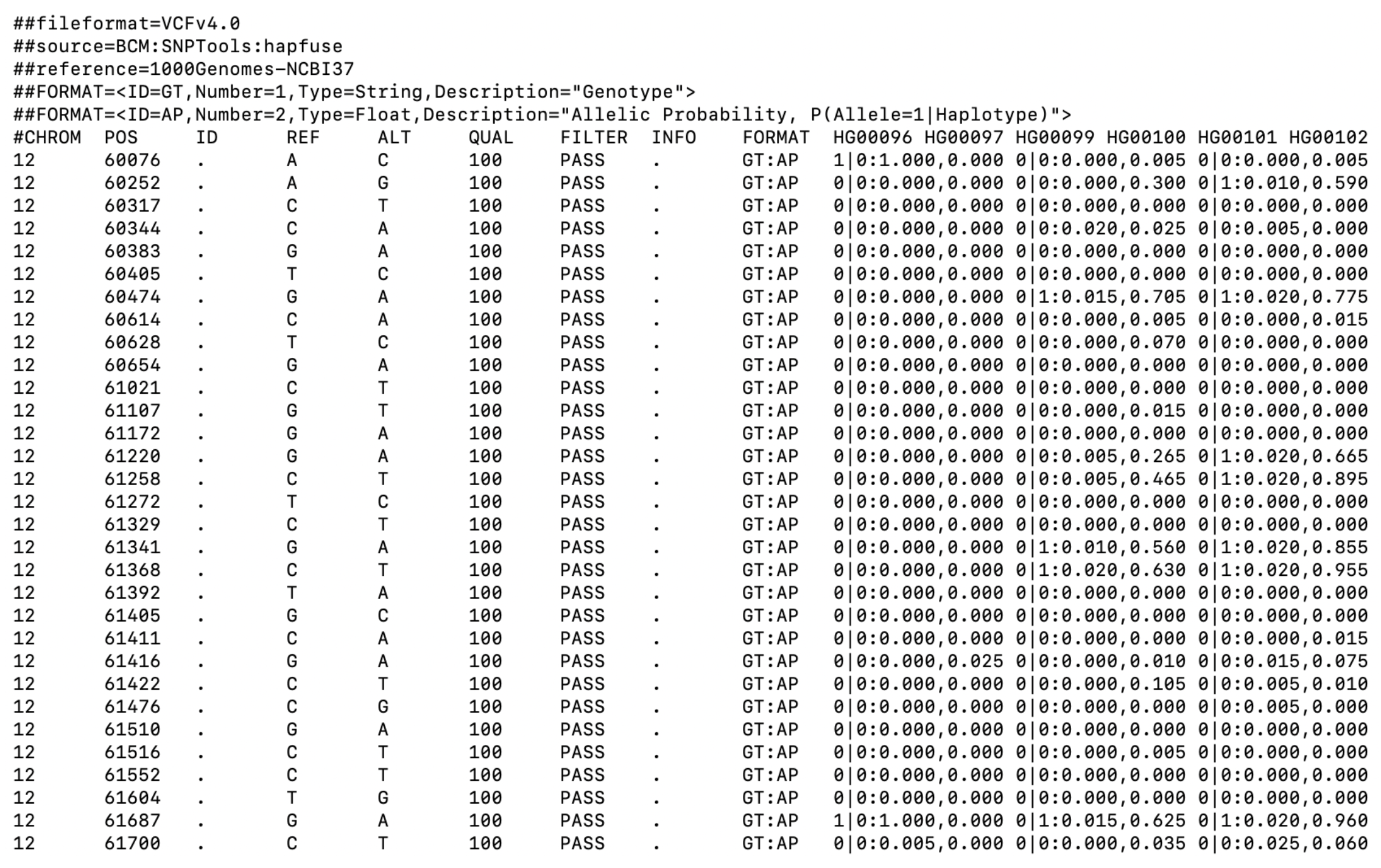
Why not VCF or a normal genotype table?

What we usually have

What we usually want

An understanding of our samples’ evolutionary history:

This is exactly what a tree sequence is!

The magic of tree sequences

They allow computing of popgen statistics without genotypes!

There is a “duality” between mutations and branch lengths.

See an amazing paper by Ralph et al. (2020) for more detail.

What if we need mutations though?

Coalescent and mutation processes can be decoupled!

What if we need mutations though?

Coalescent and mutation processes can be decoupled!

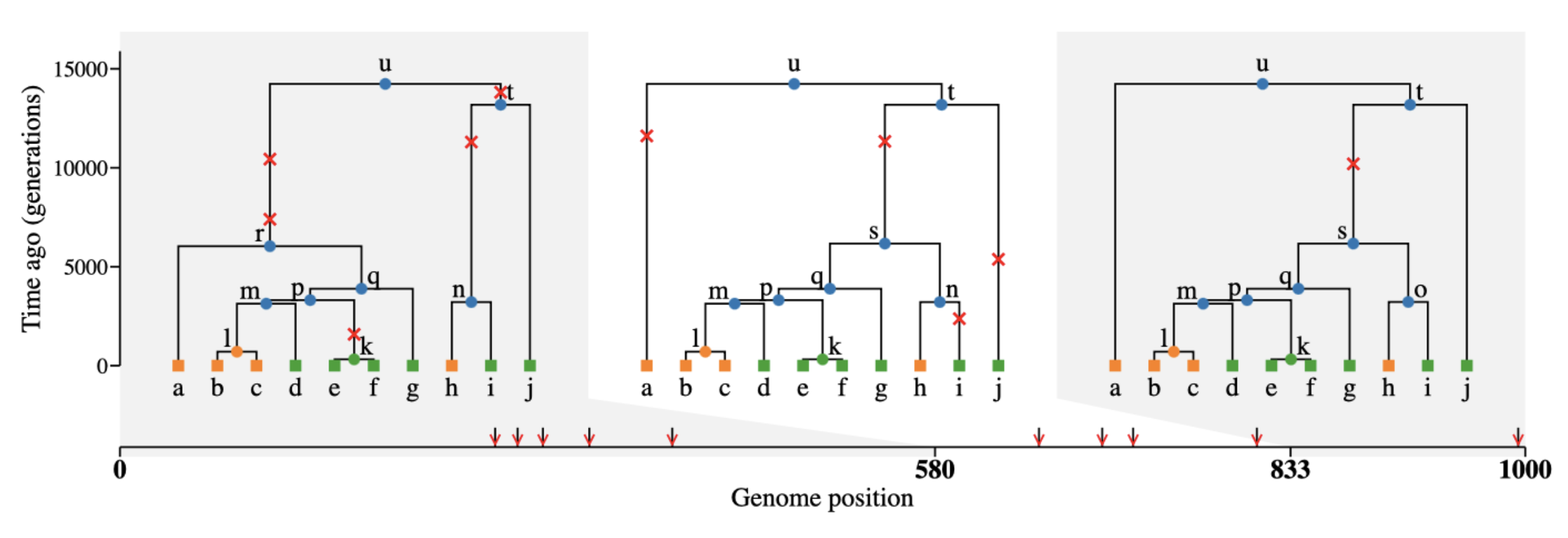
With slendr, we can add mutations after the simulation using `ts_mutate()`.

Let’s take the `model` from earlier…

… and simulate data from it

In our script we’ll have something like this:

<... population() definitions ...>

model <- compile_model(...)
  
ts <-
  msprime(model, sequence_length = 50e6, recombination_rate = 1e-8)

… and simulate data from it

In our script we’ll have something like this:

<... population() definitions ...>

model <- compile_model(...)
  
ts <-
  msprime(model, sequence_length = 50e6, recombination_rate = 1e-8) %>%
  ts_mutate(mutation_rate = 1e-8)

Always use `ts_mutate()` during exercises! Otherwise you’ll get weird results due to the lack of mutations on the tree sequence.

So we can simulate data

But how do we work with this `ts` thing?

slendr’s R interface to tskit statistics

Allele-frequecy spectrum, diversity \(\pi\), \(F_{ST}\), Tajima’s D, etc.

Find help at slendr.net/reference or in R under ?ts_fst etc.

Extracting sample information

We can get samples recorded in ts with ts_samples():

ts_samples(ts)

# A tibble: 5 × 3
  name    time pop  
  <chr>  <dbl> <chr>
1 pop1_1     0 pop1 
2 pop1_2     0 pop1 
3 pop1_3     0 pop1 
4 pop1_4     0 pop1 
5 pop1_5     0 pop1

. . .

Sometimes a shortcut ts_names() can be useful:

ts_names(ts)

[1] "pop1_1" "pop1_2" "pop1_3" "pop1_4" "pop1_5"

Example: allele frequency spectrum

Sample 5 individuals:

names <- ts_names(ts)[1:5]
names

[1] "pop_1" "pop_2" "pop_3" "pop_4" "pop_5"

Compute the AFS:

afs <- ts_afs(ts, list(names))

afs[-1]

 [1] 4267 2119 1295 1008  817  711  544  600  435  435

plot(afs[-1], type = "b",
     xlab = "allele count bin",
     ylab = "frequency")

Note: We drop the first element (afs[-1]) technical reasons related to tskit. You don’t have to worry about that here, but you can read this for more detail.

Exercise #2

Use these one-page handouts for reference.

Part a: One-population AFS simulator

In a new script model2.R write a function called simulate_afs(), which will take Ne as its only parameter.

It should create a one-population forward-time model (simulation_length 100000, generation_time 1), simulate 10Mb tree sequence (recombination and mutation rates of 1e-8), compute AFS for 10 samples and return it.

. . .

Use this function to compute AFS vectors for various Ne values. Plot those AFS and observe how (and why?) do they differ based on Ne you simulated.

Part a: Hint

You can start building model2.R from this “template”:

library(slendr); init_env()

simulate_afs <- function(Ne) {
  ... your one-population model code: population(), compile_model(), msprime() ...
  
  result <- ... compute AFS using ts_afs() on 10 samples, save it to `result` ...

  return(result)
}

afs_1 <- simulate_afs(Ne = 1000)
plot(afs_1, type ="o")

When used in R, your function should work like this:

simulate_afs(Ne = 1000)

 [1] 4000 2000 1333 1000  800  667  571  500  444  400  364  333  308  286  267
[16]  250  235  222  211  200

Part b: Estimating Ne using AFS

Imagine you sequenced 10 samples from a population and computed this AFS vector in R (# singletons, doubletons, etc.):

afs_observed <- c(2520, 1449, 855, 622, 530, 446, 365, 334, 349, 244,
                  264, 218,  133, 173, 159, 142, 167, 129, 125, 143)

. . .

You know that the population had a constant \(N_e\) somewhere between 1000 and 30000 for the past 100,000 generations, and had mutation and recombination rates of 1e-8 (i.e., parameters already implemented by the simulate_afs() function).

. . .

Guess the true \(N_e\) given the observed AFS by running single-population simulations for a range of \(N_e\) values and comparing each run to afs_observed.

Part b: Hints

Using your custom simulate_afs() function, find the value of Ne that will give the closest AFS to the observed AFS:

option #1 [easy]: Plot AFS vectors for various \(N_e\) values, then eyeball which looks closest to the observed AFS
option #2 [hard]: Simulate AFS vectors in steps of possible Ne (maybe lapply()?), find the closest AFS

Exercise #2: solution

See ex2_simple.R for a simple “eyeballing” solution.

See ex2_grid.R for a more elaborate grid-search solution.

Exercise #3

Use these one-page handouts for reference.

Exercise #3: more statistics! (a)

Use msprime() to simulate a 50Mb tree sequence ts from your introgression model in model1.R (if that takes more than two minutes, try just 10Mb).

(Remember to add mutations with ts_mutate().)

Exercise #3: more statistics! (b)

In model1.R compute (some of) these on your ts object:

nucleotide ts_diversity() in each population
ts_divergence() between populations
outgroup ts_f3(A; B, C) using CHIMP as the outgroup (A!) for different pairs of “B” and “C” populations
- using Ben’s explanation on Wednesday, try to compute this \(f_3\) using combination of \(f_2\) statistics (ts_f2(A, B))

You can find help by typing ?ts_diversity etc. into R!

Exercise #3: more statistics! (c)

Compute \(f_4\) test of Neanderthal introgression in EUR:
- Hint: check the values of these two statistics (ts_f4()):
  - \(f_4\)(<afr>, <eur>; <neand>, <chimp>)
  - \(f_4\)(<afr1>, <afr2>; <neand>, <chimp>)]
- Is one “much more negative” than the other as expected assuming introgression?
You’ve learned about symmetries in \(f_4\) depending on the arrangement of the “quartet”. How many unique \(f_4\) values involving a single quartet can you find and why? (When computing ts_f4() here, set mode = "branch").

Exercise #3: hint

For multipopulation statistics, you need a (named) list of samples recorded in each population.

ts_names() has a split = "pop" option just for this:

samples <- ts_names(ts, split = "pop")
samples

$AFR
[1] "AFR_1" "AFR_2" "AFR_3"

$NEA
[1] "NEA_1" "NEA_2" "NEA_3"

You can use this in place of sample_names in code like:

ts_diversity(ts, sample_sets = samples)

Exercise #3: solution

See ex3.R script on GitHub for a solution.

More information

slendr paper is now in PCI EvolBiol
documentation, tutorials is here
GitHub repo (bug reports!) is here

check out my new demografr inference package

contact details at bodkan.net

BONUS HOMEWORK

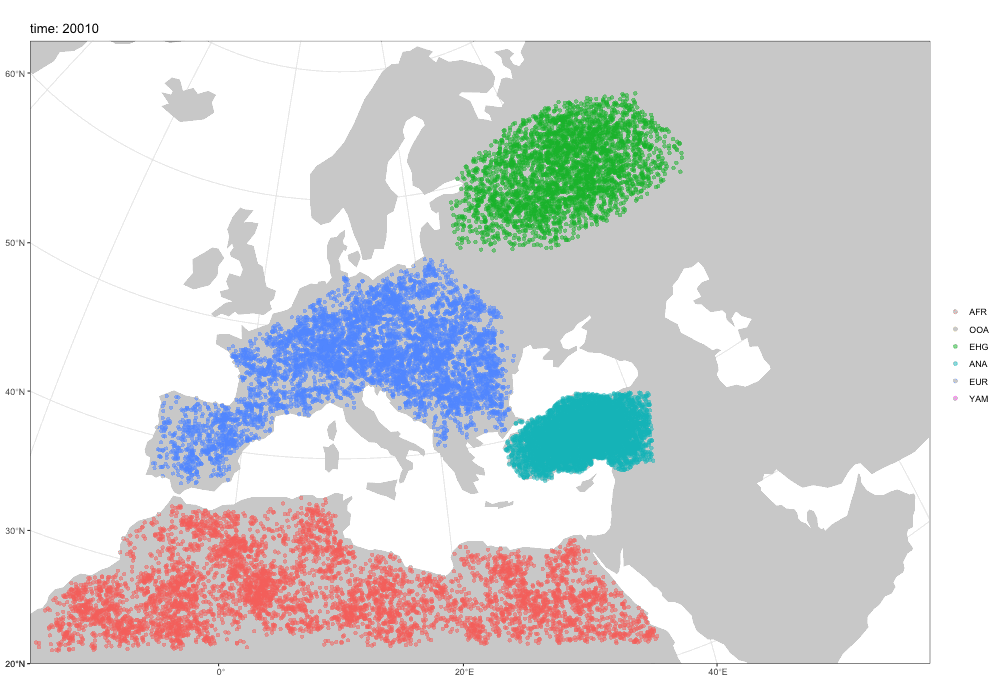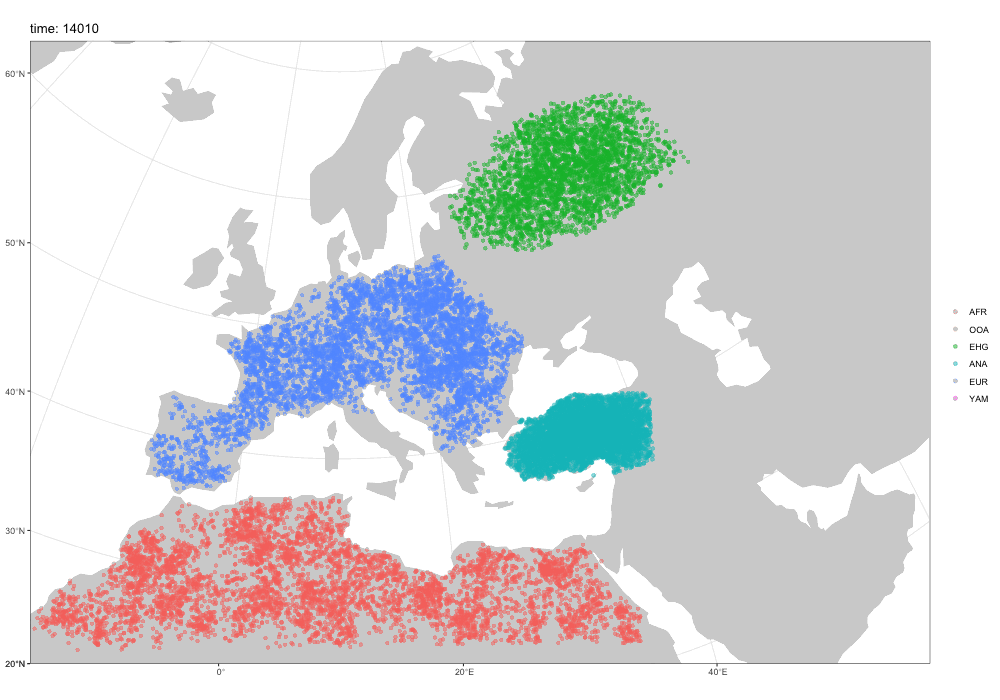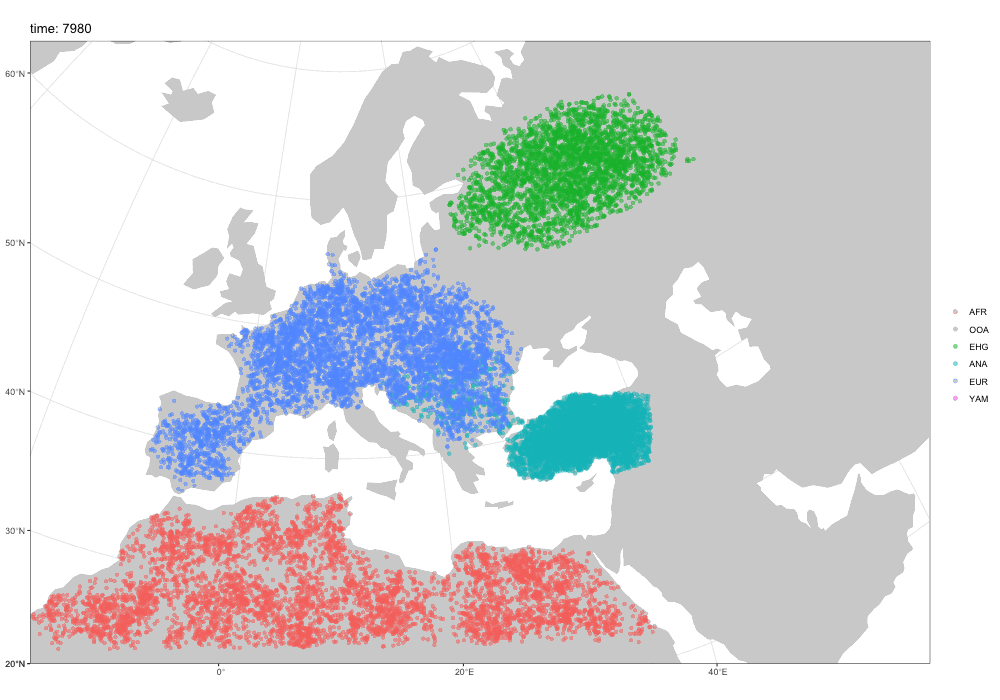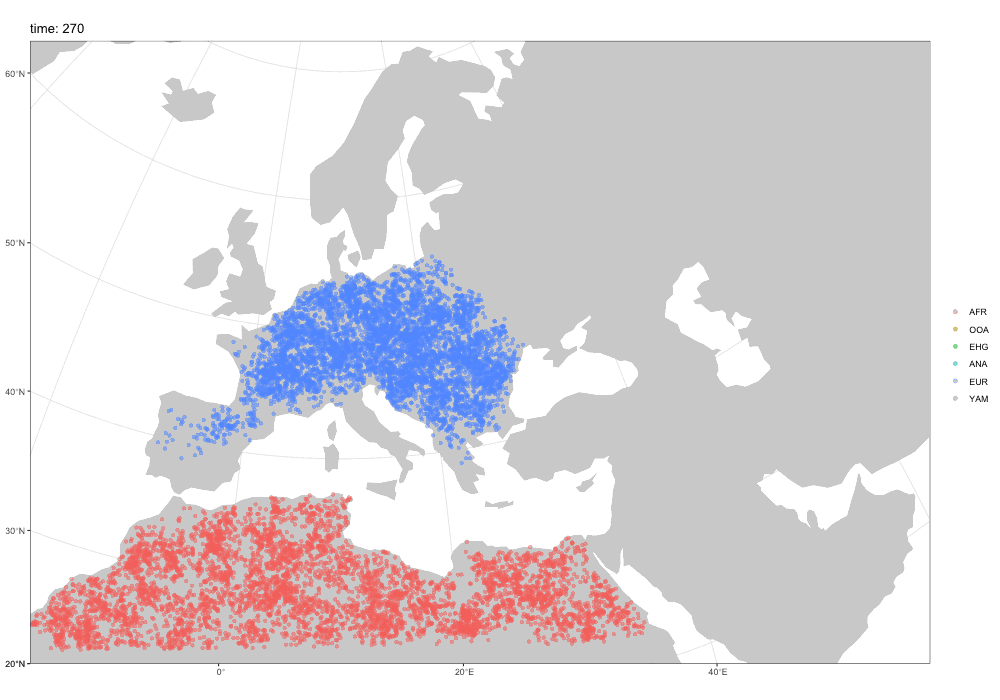
Time-series data

Sampling aDNA samples through time

Imagine we have pop1, pop2, … compiled in a model.

To record ancient individuals in the tree sequence, we can use schedule_sampling() like this:

schedule_sampling(
  model,                # compiled slendr model object
  times = c(100, 500),  # at these times (can be also a single number) ...
  list(pop1, 42),       # ... sample 42 individuals from pop1
  list(pop2, 10),       # ... sample 10 individuals from pop2
  list(pop3, 1)         # ... sample 1 individual from pop 3
)

Sampling schedule format

The output of schedule_sampling() is a plain data frame:

schedule_sampling(model, times = c(40000, 30000, 20000, 10000), list(eur, 1))

# A tibble: 4 × 7
   time pop       n y_orig x_orig y     x    
  <int> <chr> <int> <lgl>  <lgl>  <lgl> <lgl>
1 10000 EUR       1 NA     NA     NA    NA   
2 20000 EUR       1 NA     NA     NA    NA   
3 30000 EUR       1 NA     NA     NA    NA   
4 40000 EUR       1 NA     NA     NA    NA

. . .

We can bind multiple sampling schedules together, giving us finer control about sampling:

eur_samples <- schedule_sampling(model, times = c(40000, 30000, 20000, 10000, 0), list(eur, 1))
afr_samples <- schedule_sampling(model, times = 0, list(afr, 1))

samples <- bind_rows(eur_samples, afr_samples)

How to use a sampling schedule?

To sample individuals based on a given schedule, we use the samples = argument of the msprime() function:

ts <-
  msprime(model, samples = samples, sequence_length = 1e6, recombination_rate = 1e-8) %>% 
  ts_mutate(mutation_rate = 1e-8)

. . .

We can verify that only specific individuals are recorded:

ts_samples(ts)

# A tibble: 6 × 3
  name   time pop  
  <chr> <dbl> <chr>
1 EUR_1 40000 EUR  
2 EUR_2 30000 EUR  
3 EUR_3 20000 EUR  
4 EUR_4 10000 EUR  
5 AFR_1     0 AFR  
6 EUR_5     0 EUR

Exercise #4

Use these one-page handouts for reference.

Exercise #4a: ancient samples

Let’s return to your introgression model:

Exercise #4a: ancient samples

Simulate data from your model using this sampling:

one present-day CHIMP and AFR individual
20 present-day EUR individuals
1 NEA at 70 ky, 1 NEA at 40 ky
1 EUR every 1000 years between 50-5 kya

Reminder: you can do this by:

samples <- # rbind(...) together individual schedule_sampling() data frames

ts <-
  msprime(model, samples = samples, sequence_length = 100e6, recombination_rate = 1e-8) %>%
  ts_mutate(mutation_rate = 1e-8)

Exercise #4b: \(f_4\)-ratio statistic

Use \(f_4\)-ratio statistic to replicate the following figure:

Hint: You can compute Neanderthal ancestry for a vector of individuals X as ts_f4ratio(ts, X = X, "NEA_1", "NEA_2", "AFR_1", "CHIMP_1").

Exercise #4: solution

See ex4.R script on GitHub for a solution.

Standard genotype formats

If a tree sequence doesn’t cut it, you can always:

export genotypes to a VCF file:

ts_vcf(ts, path = "path/to/a/file.vcf.gz")

export genotypes in an EIGENSTRAT format:

ts_eigenstrat(ts, prefix = "path/to/eigenstrat/prefix")

access genotypes in a data frame:

ts_genotypes(ts)

1 multiallelic sites (0.064% out of 1557 total) detected and removed

  pos EUR_1_chr1 EUR_1_chr2 EUR_2_chr1 EUR_2_chr2 AFR_1_chr1 AFR_1_chr2
1 731          0          1          1          0          0          0
2 777          1          0          0          0          0          0
3 817          1          1          1          0          1          0

First things first

Why use simulations?

Making sense of inferred statistics

Making sense of inferred statistics

Fitting model parameters (i.e. ABC)

Ground truth for method development

What does it mean to simulate a genome?

If we want to simulate population genetics

The ‘genetics’ part…

The ‘population’ part…

Single-locusWright-Fishersimulation in R

“What is the expected trajectory of a neutral allele under the influence of genetic drift?”

From Fernando’s lecture on Monday…

A complete Wright-Fisher simulation

\(N\) = 500, \(p_0 = 0.5\)

Let’s make it a function

\(N\) = 500, \(p_0 = 0.5\) (20 replicates)

\(N\) = 1000, \(p_0 = 0.5\) (20 replicates)

\(N\) = 5000, \(p_0 = 0.5\) (20 replicates)

\(N\) = 10000, \(p_0 = 0.5\) (20 replicates)

\(N\) = 10000, \(p_0 = 0.5\) (100 replicates)

\(N\) = 10000, \(p_0 = 0.5\) (100 replicates)

Expected allele frequency distribution

But now for something completely different.

Let’s talk about real simulations.

There are many simulation tools

The exercises will focus on the slendrpopgen simulation toolkit for R.

What is SLiM?

Simple neutral simulation in SLiM

What is msprime?

Simple simulation using msprime

www.slendr.net

Why a new package?

Spatial simulations!

Why a new package?

Let’s get started

Everything we do will be in R

Typical steps of a slendr R workflow

Creating a population()

Programming population splits

Scheduling resize events – resize()

Tidyverse-style pipe %>% interface

A more complex model

Each object carries its history!

Gene flow / admixture

Last step before simulation: compile_model()

Last step before simulation: compile_model()

Model summary

Model visualization

Exercise #1

Go to the lecure & exercises page

Link: github.com/bodkan/ku-popgen2023

Exercise #1: write this model in slendr

Exercise #1 (bonus): your own model

Exercise #1: solution

So, now we canwrite a model

How do we simulate from it?

You don’t have to write msprime or SLiM code!

The output of a slendr simulation is a tree sequence (ts)

What is tree sequence?

Why tree sequence?

Why not VCF or a normal genotype table?

What we usually have

What we usually want

This is exactly what a tree sequence is!

The magic of tree sequences

What if we need mutations though?

What if we need mutations though?

With slendr, we can add mutations after the simulation using ts_mutate().

Let’s take the model from earlier…

… and simulate data from it

… and simulate data from it

Always use ts_mutate() during exercises! Otherwise you’ll get weird results due to the lack of mutations on the tree sequence.

So we can simulate data

But how do we work with this ts thing?

slendr’s R interface to tskit statistics

Extracting sample information

Example: allele frequency spectrum

Exercise #2

Part a: One-population AFS simulator

Single-locus
Wright-Fisher
simulation in R

But now for something
completely different.

Let’s talk about
real simulations.

The exercises will focus on the slendr
popgen simulation toolkit for R.

Creating a `population()`

Scheduling resize events – `resize()`

Tidyverse-style pipe `%>%` interface

Last step before simulation: `compile_model()`

Last step before simulation: `compile_model()`

So, now we can
write a `model`

**You don’t have to write msprime or SLiM code!**

The output of a slendr simulation is a tree sequence (`ts`)

With slendr, we can add mutations after the simulation using `ts_mutate()`.

Let’s take the `model` from earlier…

Always use `ts_mutate()` during exercises! Otherwise you’ll get weird results due to the lack of mutations on the tree sequence.

But how do we work with this `ts` thing?